Kapitel 2: Graphen
Mit Graphen lassen sich zahllose diskrete Strukturen darstellen. Zugleich beruhen sehr viele algorithmische Probleme auf der Betrachtung von Graphen. In diesem Kapitel werden wir eines davon betrachten: Wann und wie lassen sich alle Kanten eines Graphen in einem Zug ablaufen, ohne abzusetzen?
Vorlesung 2
- Datum: Dienstag, 05.11.2019
- Inhalt: Graphen und Eulertouren
- Folien: HIER (PDF, 11MB)
- Notizen: HIER (PDF, 0.9MB)
- Weitere Links:
Wikipedia-Seite zu Leonhard Euler
Archivseite zum Originalartikel von Euler
Der Originalartikel von Euler
Wikipedia-Seite zum Königsberger Brückenproblem
Wikipedia-Seite zu Graphen
Presseerklärung des MIT zur universellen Nützlichkeit von Graphen
Wikipedia-Seite: Haus des Nikolaus
(Was da nicht alles zu finden ist...)
"Heiliger Immobilienhai" (ZEIT-Illustration zum Haus des Nikolaus)
Der Nikolaus beim Architekten (Cartoon bei www.nichtlustig.de)
Webseite von Erik Demaine
Ein Artikel zum Thema Origami und Algorithmen
Vorlesungsvideos von Erik zu Algorithmen und Datenstrukturen
Vorlesung 3
- Datum: Mittwoch, 06.11.2019
- Inhalt: Wege in Graphen
- Notizen: HIER (PDF, 2MB)
- Quiz: Fragen und Resultate (PDF, 5.7MB)
Vorlesung 4
- Datum: Dienstag, 12.11.2019
- Inhalt: Notwendige und hinreichende Bedingungen für Eulertouren; Kapitelzusammenfassung
- Folien: HIER (PDF, 21MB)
- Weitere Links:
Scan der Seiten 182/3 des Buches "Das Geheimnis des kürzesten Weges" (PDF, 1,0 MB)
Seiten 184/5 (PDF, 1,1 MB)
Seiten 186/7 (PDF, 0,9 MB)
Seiten 188/9 (PDF, 1,0 MB)
Seiten 190/1 (PDF, 1,1 MB)
Wikipedia-Seite: Wege in Graphen
Wikipedia-Seite: Eulerkreise
Der Originalartikel von Hierholzer
Zum Spielen:"One touch drawing: Draw everything with only "One touch" - ein (kostenloses) Spiel, bei dem es um Eulerwege geht.
("Over 25million players can't be wrong." "Sehr gute App., um auch mal den Kopf anzustrengen." "echt ein super spiel, macht süchtig")
Für iPhone etc.
Für Android etc.
Wo wir schon dabei sind: Eine Sammlung vieler anderer kombinatorischer Spiele
Der Flynn-Effekt
 IDEA-Projekt
IDEA-Projekt
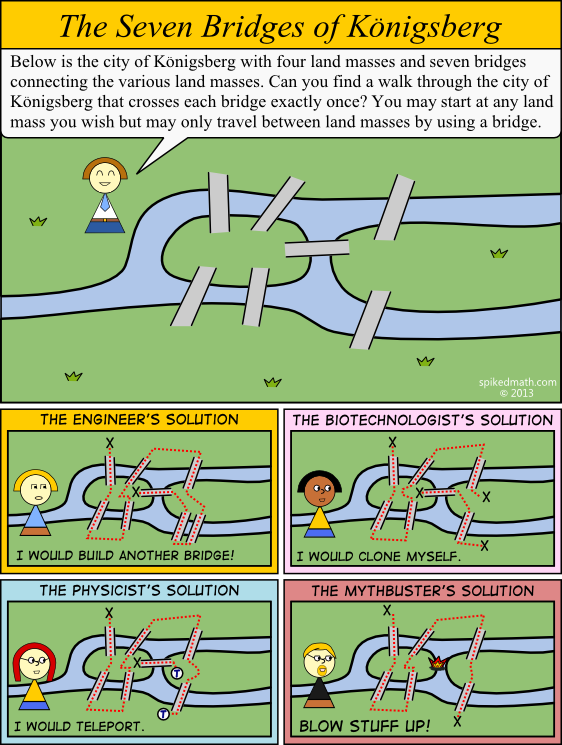
(Mathematician's solution: assuming the land patches are divided by a river, that river must originate at some point, beyond which two of the land masses are connected. The remainder of the proof is left as an exercise for the student.)
Königsberger Brückenproblem im heutigen Kaliningrad: Es geht!

Modulseiten zum Königsberger Brückenproblem und zu Leonhard Euler
Why would I ever stop doing this?!
Tuttes Gedicht über das Königsberger Brückenproblem (Basis für den Rap heute in der Vorlesung)
Michael "C." Hemmer, ehemaliges Mitglied der Algorithmikgruppe
Wikipedia-Seite: Bill Tutte
Wikipedia-Seite: Der Computer Colossus