Diese Vorlesung ist der erste Teil unserer Top-Down-Betrachtung von Programmiersprachen, bei der wir uns insgesamt vier Themen herausgreifen (Typen, Namen, Operationen und Objekte), die in der einen oder anderen Form in jeder Programmiersprache vorkommen. Im Zuge dieser Betrachtungen sollen Sie lernen, dass es grundlegende Prinzipien in Programmiersprachen gibt, die immer wieder, in unterschiedlichen Kombinationen und Geschmacksrichtungen, auftreten. Der Ingenieur baut eben doch immer das, was er kennt, bzw. er verlässt sich auf bewährte Konzepte, die häufig durch einen reichen Korpus an theoretischen Überlegungen fußen.
In dieser Vorlesung wollen wir uns mit dem Aspekt der Typen in Programmiersprachen beschäftigen. Dabei wollen wir uns zunächst überlegen, was Typen, ganz essentialistisch, sind und was die einfachsten Ausprägungen des Konzepts "Typen" sind. Dies beinhaltet, zum Beispiel, die Ganzzahl- und Zeigertypen, aber auch Record-Records, oder Verbunddatentypen, treten in vielen Sprachen auf. In C heißen sie structs. und Array-Typen. Darauf aufbauend werden wir uns dem Bereich der Polymorphie zuwenden, der ganz essentiell für unsere modernen Programmiersprachen ist. Mit diesen polymorphen Typen können wir uns ein, potentiell unendliches, Universum von Typkombinationen definieren, das dabei hilft, unsere Programme sauber zu strukturieren und uns vor uns selbst und unseren Bugs schützt. Am Ende dieser Vorlesungseinheit werden wir uns anschauen, wie die Typen, die wir in den vorherigen Kapiteln konstruiert haben, in Programmiersprachen zu einem Typsystem kombiniert werden.
Diese Vorlesung über Typen ist deswegen so spannend, weil moderne Programmiersprachen, wie C++ oder Rust, sehr ausgefeilte Typsysteme besitzen, die gewissermaßen das Rückgrat dieser Sprachen bilden. Nur mithilfe dieser rigorosen Typsysteme, die vom Übersetzer vor der Laufzeit durchgesetzt werden, ist es möglich große Programme mit vielen Entwicklern gleichzeit zu entwerfen. Typen sind dabei ein Kommunikationsmittel zwischen einem einzelnen Entwickler und der Maschine, und der Entwickler untereinander. In beiden Fällen verwendet der Programmierer die Typannotationen, um zu kommunizieren: "Beim Anlegen dieser Variable habe ich mir gedacht, dass folgende Eigenschaften und Invarianten gelten sollten".
Wenn der Entwickler mit dem Übersetzer kommuniziert, stehen zwei Aspekte von Typen im Vordergrund: der querschneidende Informationsfluss und das Explizitmachen von Erwartungen.
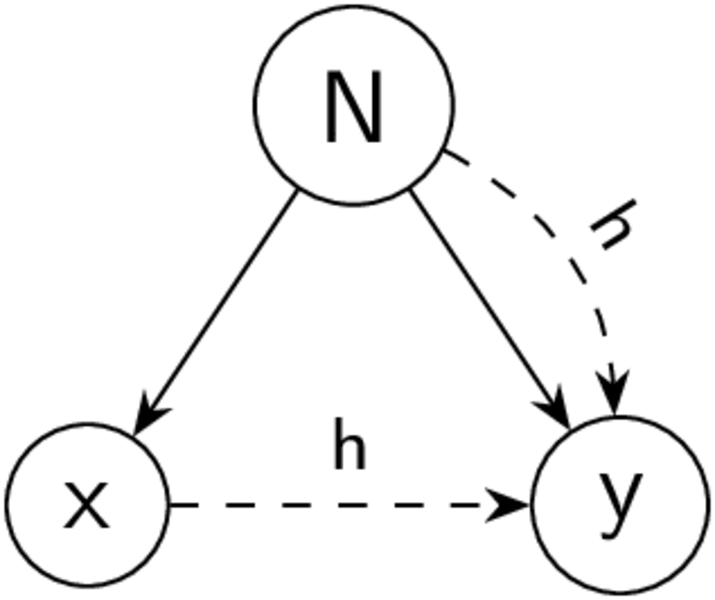
Abbildung 1: Querschneidender Informationsfluss auf einem Baum
Im Kapitel über Parsing haben wir gelernt, dass wir die Syntax unserer Maschinenprogramme kontextfrei extrahieren und als Baum darstellen können. Der große Nachteil von Bäumen ist allerdings, dass sie streng hierarchisch sind. Folgt man also nur den Kanten eines Baums, so können Informationen nur zwischen Elementen und ihren umschlossenen Kindern fließen. Es ist jedoch nicht möglich, dass Informationen von ganz vorne, nach ganz hinten, ohne besuchen der Wurzel, durchgereicht werden. Dies zeigt sich im Folienbeispiel mit dem float32_add: Würde man nur den Baumkanten folgen, so wüssten wir für a und b nicht, welche Additionsoperation wir genau verwenden sollten. In dieser Situation kommen uns Typen zur Hilfe: Durch die statische Typannotation wird der Variable an der Definitionsstelle (int32_t a) ein Kontext in den Rucksack gepackt, den sie an jeder Verwendungsstelle (a+b) mit sich herumträgt. Aus diesem Kontext, der durch die Typen etabliert wird, kann der Übersetzer dann die passende Operation auswählen. Wir haben also einen Link eingerichtet, der Quer zum Baum geht. Wie genau die Regeln für diese Links aussehen, werden wir im Kapitel über die semantische Analyse sehen.
Der zweite Vorteil von Typen ist, dass sie uns dabei helfen Bugs zu vermeiden. Denn in dem Rucksack der Variable steht nicht nur, welche Operationen an der Variable hängen, sondern auch welche Objekte gültige Belegungen für diese Variable sind. Im Beispiel kann der Übersetzer herausfinden, dass wir k1 keinen Dog zuweisen können, da Hunde und Katzen ganz unterschiedliche Typen sind. Mit der Typannotation Cat k1 macht der Programmierer die Zusicherung, dass diese Variable zu jedem Zeitpunkt, über die gesamte Laufzeit des Programms, immer nur Katzen speichert.
Der dritte Vorteil von Typen betrifft die Kommunikation mit anderen Menschen. Ohne die Angabe von Typen muss der lesende Programmierer sich überlegen, von welcher Art die gespeicherten Objekte sind. Mit Typen, die vielleicht sogar noch, wie im Beispiel, sprechende Namen haben, ist es deutlich einfacher, ein Programm zu verstehen.
Zusammengefasst möchte ich also sagen: Sehen Sie Typen und das Typsystem Ihrer Programmiersprache nicht als Feind, der Sie davon abhält, sich auszudrücken, sondern als Freund und Helfer in der Not, der Sie davon abhält dumme Dinge zu tun.
Als ersten Schritt unserer Betrachtung über Typen werden wir uns die Frage stellen: "Was ist so ein Typ überhaupt?". Was ist also die Essenz von Typen, wenn wir all die Spezifika von einzelnen Sprachen wegabstrahieren? Welche Definition legen wir an, um alle Typen in allen Programmiersprachen zu erfassen? Dazu gibt es allerdings nicht nur eine definitive Antwort, sondern drei verschiedene Sichtweisen (strukturell, denotationell, und abstraktional), die alle nützlich sind und verschiedene Aspekte beleuchten.
Die strukturelle Interpretation von Typen ist eine sehr technische Herangehensweise an das Problem. Sie beantwortet die Frage "Was sind Typen?" damit, dass alles ein Typ ist, was ich nach den Regeln der Typkomposition bauen kann. Das ist in etwa so, wie wir sagen können, dass positive Ganzzahlen jene mathematischen Objekte sind, die ich durch fortwährendes Inkrementieren, ausgehend von der 1, erzeugen kann. Oder, dass all jenes ein Brot ist, was ich durch Mischen und Backen von Mehl mit Wasser erzeugen kann (später kommen wir wieder auf das Brotthema zurück, versprochen!). Im Falle von Typen kommt dieses konstruktive Argument dann zu so Schlüssen wie "Pointer auf char" ist ein Typ, weil char ein Typ ist und "Pointer auf X" eine Kompositionsregel für Typen ist.
Bei der strukturellen Interpretation bilden Typausdrücke eine zentrale Rolle. Sie beschreiben, wie wir komplexere Typen aus einfachen Typen mittels der Anwendung von Typkonstruktoren erstellen. Dabei muss die Sprache eine Menge von eingebauten Basistypen (built-in types) mitbringen, die bereits definiert sind, bevor ein einziges Zeichen Code interpretiert wurde. Häufig enthält diese initiale Bevölkerung der Menge aller Typen (die Menge T) bereits Ganzzahlentypen, Zeichentypen und einen Typ für Wahrheitswerte.
Typkonstruktoren sind dann Funktionen, die eins oder mehrere Elemente der Typmenge als Argumente bekommen und einen neuen Typausdruck erzeugen, der wieder Teil der Menge T wird. Dabei mag es den geneigten Leser verwundern, dass wir nicht den Rückgabewert der Typkonstruktoren angeben, sondern den noch nicht ausgewerteten Ausdruck. Dies tun wir, da uns nicht konkrete Bitrepräsentation von Typen in einem konkreten Übersetzer interessiert, sondern wie diese Typen gebildet werden. Unser "Pointer auf char" von eben würden wir also als pointer(char) aufschreiben. Um dies zu verdeutlichen, wollen wir uns kurz ein Stück Python anschauen, mit dem wir diese strukturelle Interpretation betrachten können:
# Built-in Types BOOL = 0 CHAR = 1 INT = 2 # Typkonstruktoren def POINTER(pointee_type): return (100, pointee_type) def PAIR(T1, T2): return (101, T1, T2) def SET(element_type): return (102, element_type) # Typausdrücke print "char: ", CHAR print "pointer to char:", POINTER(CHAR) print "pair of int and set of char:", PAIR(INT, SET(CHAR))
In diesem minimalen Typsystem sehen wir schon mehrere Dinge: Die Existenz von built-in Typen, die Anwesenheit von Typkonstruktoren, und den Unterschied zwischen dem Typausdruck (POINTER(CHAR)) und der Kodierung des Typens als Objekt (100, 1). Prinzipiell können wir mit diesem Typsystem schon unendlich viele Typen erzeugen, indem wir die Konstruktoren, wie POINTER, immer und immer wieder anwenden. Dabei entstehen immer tiefer geschachtelte Typausdrücke.
Zur strukturellen Sicht gehört auch, dass wir diese Typausdrücke, aufgrund ihrer Schachtelung, als Baum aufmalen können. Dabei sehen sie strukturell sehr ähnlich zu unserem AST aus dem letzten Kapitel aus; ein Fakt, dem wir im Kapitel über die semantische Analyse noch einmal begegnen werden.
Die zweite Brille auf Typen ist die denotationelle Sicht auf Typen. Mit diesem Blick definieren wir einen Typ als ein Prädikat über alle möglichen (imaginären und realen) Objekte (object) des Universums. Sagt das Prädikat "ja", so ist das Objekt von diesem Typen, sagt es nein, so liegt es außerhalb der Umschlossenen Objektmenge des Typen. Mit dieser Brille sind Typen viel viel flexibler gefasst als mit der rein strukturellen Sicht, weil wir einfach irgendein Prädikat angeben müssen, um einen Typen zu definieren. So kann die Menge aller geraden Zahlen ein eigener Typ int_even sein:
def int_even(obj): if type(obj) is int and (obj % 2) == 0: return True return False objects = [1, 2, 3, "foo", True, [1,2,3]] # + range(4, 20) # Zermelo Fraenkel: [ obj | obj <- objects, int_even(obj) print [obj for obj in objects if int_even(obj)]
Hier nutzen wir das Prädikat, um eine Liste von Objekten auf jene Objekte zu filtern, die vom entsprechenden Typen sind. Beachten Sie, wie wir in unserem Prädikat die Python-Primitive type() verwendet haben, um unser Prädikat aus einem Basistypen abzuleiten.
Wenn wir die Regeln eines denotationell definierten Typs strukturierter aufschreiben als mittels einer Python-Funktion, so kann ein Übersetzer daraus auch Eigenschaften der Objektmenge herleiten. So könnte der Optimierer bei der Addition zweier int_even Variablen wissen, dass das Ergebnis auch wieder int_even sein wird.
Die dritte Interpretation von Typen ist die abstraktionale Sicht. Dabei wird ein Typ als eine Menge von validen Operationen auf Objekten des Typen definiert. Hier wird die Idee des Typkontexts, die wir vorhin aufgegriffen haben (Rucksack), besonders deutlich. Der Typ ist sein Interface, egal wie dieses Interface implementiert ist. Eine Beispiel für die abstraktionale Definition von Typen sind die Interfaces in Java:
interface Object2D { float area(); } class MyMain { public static void main(String[] args) { Object2D obj = ....; obj.area(); } }
Hier definieren wir das Interface Object2D, welches durch die Methode float area() festgelegt ist. Im späteren Verlauf können wir dann Variablen anlegen, die alle Objekte aufnehmen können, die dieses Interface implementieren. Durch Nutzung des Interface-Typs haben wir über die Variable obj die Garantie, dass es eine area()-Methode gibt, die eine Gleitkommazahl liefert.
Mit unseren drei Brillen haben wir nur eins geschafft: Wir haben Typen geschaffen, aber bisher können wir mit ihnen nichts anstellen. Ziemlich nutzlose und faule mathematische Objekte, sich einfach wild von uns erzeugen zu lassen. Daher wollen wir nun, neben den Typkonstruktoren, weitere Operationen definieren, die auf unserer Typmenge arbeiten. Möglichst nützliche Operationen.
Die wahrscheinlich wichtigste Frage für einen Übersetzer ist, ob zwei gegebene Typen äquivalent sind. Also, ob sie das gleiche bedeuten. Wenn zwei Typen äquivalent sind, so sind ihre Objekte aus Sicht des Typsystems nicht unterscheidbar, vollständig kompatibel zueinander und sowieso best-friends-forever. Oder um es etwas ausgewählter zu formulieren: Typäquivalenz ist die strikteste Relation zwischen zwei Typen. Dabei gibt es zwei unterschiedliche Arten der Typäquivalenz, die in Programmiersprachen auftreten können: Die Strukturäquivalenz und die Namensäquivalenz.
Bei der Strukturäquivalenz sind zwei Typen äquivalent, wenn sie den gleichen Typausdruck haben. Wenn wir in einem Programm einen Typnamen verwenden (Pascal type NAME = ...), so ist das nur eine Abkürzung für den Typausdruck auf der rechten Seite, der NAME selbst wird beim Vergleich ignoriert. Weiterhin werden unterschiedliche Notationen, solange sie zum selben Typausdruck führen, als äquivalent angesehen.
Diese sehr technische Art der Äquivalenz hat allerdings einige gravierende Nachteile, weswegen sie heute kaum noch verwendet wird. Das erste ist, dass es zu einer zufälligen, nicht intendierten Äquivalenz kommen kann, wenn zwei Typen aus Versehen die gleiche Struktur haben. So ist der Typ student und der Typ school auf den Folien in Pascal, welches strukturelle Äquivalenz verwendet, gleich, obwohl die Intention ganz deutlich, durch zwei Typdefinition, war, dass der Programmierer unterschiedliches meinte.
Das zweite Problem struktureller Äquivalenz sind rekursive Datentypen. Solche rekursiven Typen können auftreten, wenn wir Typen einen Namen geben können und diesen Namen in der Definition des Typs selbst verwenden. Das Paradebeispiel eines rekursiven Typs, den wir auch schon im Parsing-Kapitel besprochen haben, ist die verkettete Liste, bei der jedes Listenelement einen Pointer auf eine (Rest-)Liste beinhaltet. Das Problem entsteht dann, wenn wir jedes Auftreten des Typnamens einfach durch den Erzeugten Typausdruck ersetzen wollen, weil dann ein endlos tief geschachtelter Typausdruck für diese doch sehr einfache Liste entsteht. Zwar wäre eine endlose Struktur für den Mathematiker erst mal in Ordnung, doch man muss einige TricksThe Equivalence of Modes and the Equivalence of Finite Automata anwenden, um solche unendlichen Typausdrücke auf einem endlichen Rechner zu vergleichen.
Aufgrund dieser Probleme mit struktureller Äquivalenz verwenden die meisten modernen Sprachen Namensäquivalenz. Die Idee dabei ist, dass jede Definition eines Typs, egal wie der Typ strukturiert ist, ein eigener Typ ist, der nur äquivalent zu sich selbst ist. Wenn der Programmierer sich schon die Mühe macht einen Namen auszusuchen, dann sollten wir immerhin sagen, dass dieser Typ was besonderes ist!
Immer wenn ein Typname in einem Typausdruck verwendet wird, speichern wir dort nur den Namen, nicht den zugewiesenen Typausdruck, womit unsere Typausdrücke, selbst für rekursive Typen, wieder hübsch hierarchische Bäume werden.
Zusammen mit Namensäquivalenz kommt dann sofort die Frage auf, ob wir Aliase von Typen erstellen können: Ein Typalias ist ein zweiter Typname, der den selben Typen (nicht nur den gleichen Typausdruck) referenziert und damit voll äquivalent ist. So kann man in der Sprache C, die für Records Namensäquivalenz verwendet, mittels typedef einen Typalias erzeugen. In C ist typedef sogar die einzige Methode einen neuen Typnamen zu definierenSiehe Lexer Hack..
Es ist wichtig zu verstehen, dass alle typedef auf den gleichen Typausdruck äquivalent sind und keine Unterscheidung machen. Dies bedeutet, dass (auf den Folien) celsius_t und fahrenheit_t der gleiche Typ (double) ist. Daher kann uns der Übersetzer nicht dabei helfen, eine Fehlverwendung von heating_set zu erkennen. Ein ähnlicher Fehler hat die Menschheit schon einen Mars Climate Orbiter gekostet.
Eine Möglichkeit dies in C zu lösen sind Records mit nur einem Feld. Da für struct Namensäquivalenz gilt, kann man auf diese Art nicht-äquivalente Typen erzeugen, bei denen der Übersetzer prüft, ob wir sie aus Versehen vermischen. Zum Beispiel verwendet der Linux Kern eine Typdefinition für atomic_t mit der verhindert wird, dass man aus Versehen einen atomaren Datentyp mittels ++ hochzählt und sicherstellt, dass man stattdessen die spezielle API atomic_add(int i, atomic_t *v) verwendet.
typedef struct { volatile int counter; } atomic_t;
Andere Sprachen wie z.B. Ada erlauben es nicht nur Typaliase anzulegen (subtype), sondern auch Typen, die nicht-äquivalent sind, aber den selben Typausdruck haben, mittels type anzulegen.
Nachdem wir eine Idee davon haben, wie man den Begriff des Typen definiert und was man prinzipiell damit machen kann, wollen wir uns nun einige Typen anschauen, die ganz "typisch" sind und in vielen Programmiersprachen vorkommen. Diese Typen sind ein Basisset, was man als Programmierer von einer Sprache erwartet bzw. erwarten darf. Dennoch ist es so, dass nicht jede Sprache diese Typen als built-in Typen bereit stellt. Häufig werden sie durch Bibliotheken der Typmenge hinzugefügt. So ist es zum Beispiel typisch, dass der Listentyp nicht in die Sprache eingebaut ist, sondern mittels einer rekursiven Struktur als einfach verkettete Liste "nachgebaut" wird. An dieser Stelle merken wir bereits, wie die Komposition von built-in Typen uns erlaubt, neue Abstraktionen auf bereits Bestehendem zu schaffen.
Die Klasse der geläufigen Typen (um nicht immer typische Typen schreiben zu müssen), lässt sich grob in zwei Kategorien aufteilen. Zum einen haben wir die skalaren Typen, die genau ein Objekt beschreiben, das sich nicht weiter sinnvoll unterteilen lässt. Die Objekte der skalaren Typen werden also immer "als ganzes" im Programm herumgereicht und verwendet. Im Gegensatz dazu gibt es die zusammengesetzen Typen, die sich aus mehreren erst mal logisch unabhängigen Objekten zusammensetzen. Bei diesen Typen ist es möglich, dass ein Teil des Objekts herausgelöst vom Rest betrachtet und herumgereicht werden kann.
Bei einigen Typen lässt sich darüber streiten, ob sie nun skalar oder zusammengesetzt sind. So kann ein Typ technisch zusammengesetzt sein (weil er als Record implementiert ist), aber dennoch intentional skalar sein, weil er nur als Einheit herumgereicht werden soll. Ein Beispiel hierfür ist der C++ std::shared_ptr.
Die wichtigsten skalaren Typen sind die numerischen Typen, die wir verwenden, um Zahlen darzustellen und die in ihrem Abstraktionenrucksack die arithmetischen Operationen mit sich herumtragen. Durch diese Typen scheint ganz häufig die technische Informatik und die Implementierung von arithmetischen Operationen auf dem realen Prozessor durch. So haben die ganzen Zahlen häufig einen endlichen Wertebereich, der sich an der Granularität des Speichers (1 Bytes sind 8 Bit) und der Wortbreite (8, 16, 32, 64 Bit) orientiert. Wir finden mit diesen Typen also Typen wieder, die auch die reale Maschine versteht und effizient speichern und verarbeiten kann. Neben der Anzahl der verfügbaren Bits ist für den Wertebereich der ganzzahligen Typen noch wichtig, ob sie mit Vorzeichen (signed) oder ohne Vorzeichen (unsigned) gespeichert werden sollen. Häufig definiert hier die Programmiersprache noch, dass vorzeichenbehaftete Ganzzahlen im Zweierkomplement gespeichert werden, weil hierfür effiziente Hardwareoperationen zur Verfügung stehen.
Ein wichtiger Punkt bei diesen numerischen Typen ist die Frage: Was passiert eigentlich, wenn der Wertebereich überschritten wird. Also was passiert, wenn ich bei einem int8_t, der gerade den Wert 127 hat, eins aufaddiere? An dieser Stelle kann eine Programmiersprache sehr unterschiedliche Entscheidungen treffen: Die eine Möglichkeit ist, dass sie ein Überlaufverhalten definiert und bestimmt, dass (int8_t)127++ zum Wert -128 führt. Dadurch klopfen wir allerdings auch fest, dass die ganzen Zahlen das Verhalten des Zweierkomplements zeigen müssen. Soll ein Programm nun aber auf einer Einerkomplementmaschine ausgeführt werden, so muss der Übersetzer das Verhalten des Zweierkomplements aufwendig emulieren, um die versprochene Sprachsemantik zu erfüllen. Die andere Möglichkeit, die zum Beispiel von C gewählt wird, ist den Ganzzahlüberlauf als undefiniertes Verhalten zu markieren. Dies bedeutet, dass der Übersetzer frei entscheiden kann, was passiert, wenn eine vorzeichenbehaftete Ganzzahl überläuft. Auf diese Weise können Ganzzahlen sowohl auf einem Rechner mit Einerkomplement als auch auf einem Zweierkomplementrechner effizient verarbeitet werdenInteger Overflows sind allerdings ein schwerwiegendes Problem in real existierender Software. Understanding Integer Overflow in C/C++, Dietz et. al., TOSEM 2015.
Neben den ganzzahligen Typen gibt es dann normalerweise noch Gleitkommazahlen mit einfacher Genauigkeit (float, 32 Bit) und doppelter Genauigkeit (double, 64 Bit). Diese Gleitkommazahlen haben eine wechselnde Genauigkeit über ihren ganzen Wertebereich, weswegen für Finanzanwendungen noch Festkomma- und Dezimalzahltypen zur Verfügung stehen können. Bei den Dezimalzahlen mit festem Komma gibt der Typ dann nicht die Anzahl der verwendeten Bits an, sondern wie viele Dezimalstellen vor und nach dem Komma präzise gespeichert werden. So kann der Typ DECIMAL(6,2) in der MySQL Datenbank alle Zahlen von -9999.99 bis 9999.99 auf den Cent genau speichern.
Zusätzlich zu den Zahlen mit endlichem Wertebereich gibt es auch noch die bignum Typen. Bei diesem Typen garantiert die Sprache, dass es niemals zu einem Überlauf kommt. Technisch wird, wenn die Zahl überlaufen würde, einfach mehr Speicher allokiert. Ein Beispiel für so eine Sprache, die implizit von Ganzzahlen endlicher Länge auf bignums wechselt, ist Python:
import sys MAX_INT = sys.maxsize # Der größte Integer der als <type 'int'> dargestellt werden kann. # <type 'int'> hat endliche Länge # <type 'long'> ist ein Bignum print [type(1), type(MAX_INT), type(MAX_INT+1), type((MAX_INT+1)-1)]
Außerdem gibt es dann noch die Aufzählungstypen, bei denen der Entwickler selbst einen Typ als eine Menge diskreter Werte definieren kann. Diese Typen sind nützlich, wenn eine Menge von Werten mit lesbaren Namen versehen werden soll. Häufig garantiert die Sprachsemantik dann noch, dass die Elemente dieser Aufzählung eine totale Ordnung haben und man, im Beispiel red < green machen kann. Dies rührt daher, dass die Aufzählungstypen normalerweise auf Ganzzahlen abgebildet werden. Bei manchen Sprachen ist die Abstraktion der Aufzählungstypen allerdings löchrig und man kann einer Variable vom Aufzählungstyp auch einen Wert zuweisen, der nicht in der Aufzählung vorkommt:
typedef enum {red, green, blue} color_t; color_t invalid_color = 1000;
Weiterhin sind auch die Zeiger- bzw. Referenztypen skalar. Die Objekte dieser Typen sind nicht an sich nützlich, sondern sie enthalten Referenzen auf andere Objekte. Im Beispiel ist der Wert 0x1234 das Zeigerobjekt selbst und es referenziert das Objekt 500. Um diese Referenzierung ins Typsystem einzubinden, sagt ein Zeigertyp häufig nicht nur "ich bin eine Referenz", sondern auch "ich bin eine Referenz auf ein Objekt vom Typ X". In unserem Fall haben wir einen pointer(int) vor uns; das referenzierte Objekt ist also immer ein int, niemals ein double.
Als kleinste Menge an Abstraktionen muss ein Zeigertyp, um nützlich zu sein, dereferenziert werden können. Durch das Dereferenzieren kommen wir zur Laufzeit zum referenzierten Objekt. Spannend an diesem dereference-Interface ist seine parametrische Schreibweise, bei der die Signatur andeutet, dass der Pointee-Type T aus dem Typausdruck pointer(T) ausgepackt und als Rückgabetyp verwendet wird. Mehr zu dieser Art der Typmuster werden wir im Unterkapitel über Polymorphie lernen.
In Sprachen kann es unterschiedliche Arten von Referenztypen geben, die neben der reinen Objektreferenz noch weitere Eigenschaften haben. So gibt der C++-Referenztyp T& die Garantie, dass immer ein valides Objekt referenziert ist. Der std::unique_ptr stellt hingegen sicher, dass es immer nur eine Referenz für das referenzierte Objekt zu einem Zeitpunkt gibt. Dies bedeutet, dass der Besitzer des std::unique_ptr auch das Objekt alleinig "besitzt".
Im Zoo der skalaren Typen spielen die Funktionstypen eine ganz zentrale Rolle, wenn auch eine sehr sonderbare, denn Funktionsobjekte können nicht verändert werden und nur ganz wenige Sprachen erlauben das Anlegen neuer Funktionsobjekte zur Laufzeit (JavaScript und Python sind Beispiele hierfür). Ein Funktionstyp beschreibt das Interface, das eine Funktion aufweist: Also welche Typen haben die Parameter, und was ist der Rückgabetyp. Jede Funktion hat einen Funktionstyp, der direkt aus ihrer Signatur, durch weglassen der Parameternamen, berechnet werden kann. Die einzige Operation auf einem Funktionstyp ist der Aufrufoperator call, der eine Funktion mit ihrer Argumentliste füttert und den Rückgabewert, korrekt typisiert mit R, zurückliefert.
Eigentlich können wir Funktionstypen nicht verwenden, um Variablen zu typisieren: Da wir keine neuen Funktionsobjekte anlegen können, können wir sie auch nicht zuweisen bzw. kopieren. Daher können wir höchstens einen Zeiger auf ein Funktionsobjekt, einen Funktionszeiger, herumreichen: pointer(func(size_t, pointer(char))). Da diese strikte Trennung zwischen Funktion und Funktionszeiger allerdings eher müßig ist, wird häufig nicht besonders Trennscharf zwischen Funktion und Funktionszeiger unterschieden.
Ein anderer wichtiger Aspekt, der nicht offensichtlich ist, aber der eigentlich aus der Orthogonalität von Typkonstruktoren hervorgeht ist, dass wir Funktionstypen definieren können für Funktionen die (Zeiger auf) Funktionen zurückgeben: func(func(size_t, pointer(char)), int). Dieser Typausdruck besagt, dass die Funktion einen int übergeben bekommt und eine Funktion vom Typ func(size_t, pointer(char)) zurückliefert. Zumindest in C ist die Syntax für solche Funktionen allerdings mehr als unintuitiv, weshalb man dort lieber ein typedef verwenden sollte:
#include <string.h> size_t (*func(int param)) (const char* ) { return &strlen; } typedef size_t (*func_ptr_t)(const char*); func_ptr_t func2(int param) { return &strlen; }
In Sprachen, in denen Funktionen als Rückgabewert häufiger vorkommen, gibt es deutlich intuitivere Notationen für solche Funktionstypen. In Haskell-Notation wäre diese Funktion dann:
func:: int -> const char* -> size_t -- '->' ist Rechtsbindend und daher äquivalent zu: func:: int -> (const char * -> size_t)
Die anderen geläufigen Typen sind die zusammengesetzten Typen. Die Objekte dieser Typen bestehen aus mehreren Subkomponenten/Elementen, die auch herausgelöst Sinn ergeben. So hat eine Liste viele Listenelemente; jedes einzelne Listenelement ergibt auch ohne die Liste einen Sinn. Es gibt, ganz allgemein gesprochen, drei verschiedene Kategorien von komponierenden Typen: Strukturen, Sequenzen und Abbildungen.
Bei den Record-Typen (oder Strukturtypen) sind die Subkomponenten eindeutig benannt (name), aber ihre Anzahl ist endlich und Teil des Typausdrucks. Durch diese eindeutige Benennung der Elemente ist zu jedem Zeitpunkt eine eindeutige Wiederauffindbarkeit, anhand des Strukturtyps und des gegebenen Namens, gewährleistet. Das Wiederauslesen der Elemente geschieht durch den dot_operator, der den Typausdruck des Strukturtypen inspiziert: Auf Ebene der Objekte holt der Operator das Element mit dem entsprechenden Namen heraus und gibt es zurück. Auf Ebene der Typen hat der Operator den Elementtyp mit dem entsprechenden Namen als Rückgabetypen. Wenn der Rückgabetyp des dot_operators eindeutig und zur Übersetzungszeit festgelegt sein soll, was für die meisten übersetzten Sprachen der Fall ist, so muss der name eine Konstante sein. Etwas, was dadurch erreicht wird, dass man Bezeichner als Strukturtypnamen verwendet. Alle anderen Regeln, die für Strukturtypen gelten, wie dass die Elemente in einer gewissen Ordnung gespeichert werden, sind sprachspezifisch.
Um das ganze etwas plastischer zu machen, wollen wir uns ansehen, wie C-struct-Typen auf unser Modell von Strukturtypen passen:
typedef struct { int feld_1; double feld_2; } foo_t ; // type foo_t // = record((int, field_1), // (double, field_2)) ... struct foo_t var; var.feld_1 = 1; // dot_operator(foo_t, feld_1) -> int var.feld_2 = 1.5; // dot_operator(foo_t, feld_2) -> double
Der Strukturtyp hat zwei Elemente mit den Namen "feld_1" und "feld_2"; beide Elemente haben unterschiedliche Typen (int, double). Der dot_operator ist als . in der Sprache als Infixoperator eingebaut. Im Beispiel extrahiert der Ausdruck var.feld_1, das Feld feld_1 aus dem Objekt, welches in var gespeichert ist. Dabei ist der Feldname fix und nur das Objekt veränderlich.
Es gibt zwei geläufige Sonderformen von Strukturtypen: Tupel und varianten Records. Bei Tupeln sind die Elemente nur implizit über ihre Position im Tupel benannt; der Benutzer muss sich keinen expliziten Namen ausdenken. Bei varianten Records, in C union, ist zur Laufzeit immer nur ein Element gültig und alle Elemente teilen sich den gleichen Speicherplatz.
Der zweite geläufige zusammengesetzte Typ sind Sequenzen. Bei Sequenzen erlauben wir, dass die Anzahl der Elemente zur Laufzeit variabel und potentiell unendlich ist. Um dennoch eine eindeutige Typisierung zu bekommen, verlangen wir, dass alle Elemente der Sequenz den gleichen Typ haben. Um auf die Elemente von Sequenzen zugreifen zu können, muss die Sequenz zwei Operationen (head, tail) anbieten. Dabei liefert head ein Element, bei geordneten Sequenzen das erste, und tail eine Sequenz mit allen anderen Elementen zurück.
Die einfachste Variante eines Sequenztyps ist die einfach verkettete Liste, über die wir schon genug geredet haben. Aber auch andere Sequenzen wie eine priorisierte Warteschlange (Java: PriorityQueue<T>) oder eine ungeordnete Menge (Java: HashSet<T>) fallen in die Kategorie Sequenzen. In jedem Fall können wir eins ums andere Element aus der Sequenz entfernen und sind uns immer sicher, ein Objekt vom Typ T in den Händen zu halten.
Die dritte Variante von zusammengesetzten Typen sind die Abbildungstypen. Ihr Typkonstruktor map(K,V) bekommt (mindestens) zwei Typen als Argument, die die Indexmenge (K) und die Wertemenge (V) der Abbildung typisieren. Beide Mengen sind, wie bei den Sequenzen, homogen typisiert. Der Zugriff auf die Elemente von Abbildungen erfolgt, anderes als bei Sequenzen, wahlfrei durch get(), welches aus einem Abbildungsobjekt und einem Objekt der Indexmenge das vorher zugewiesene Objekt der Wertemenge liefert. Da sowohl Indizes als auch Werte homogen typisiert sind, ist die Signatur von get() anhand des Typausdrucks des Abbildungstypen eindeutig. Etwas informeller ausgedrückt: Mit Abbildungen kann ich etwas unter einem Index speichern und unter dem gleichen Index wiederfinden.
Der wohl geläufigste Abbildungstyp, den man zuerst nicht als solchen identifiziert, ist das Array. Bei Arrays ist der Datentyp der Indexmenge auf int festgelegt, die Indexmenge ist kompakt (ohne Lücken) und muss beim Erstellen der Abbildungsobjekte angegeben werden. Dies geschieht durch die Angabe der Arraygröße und den Startindex. Häufig ist der Startindex noch per Sprachregel, wie bei C, auf 0 festgetackert. Allerdings wird die Zugehörigkeit von Arrays zu den Abbildungstypen klarer, wenn wir uns anschauen, dass es Sprachen wie Pascal gibt, die es dem Programmierer erlauben, den Startindex frei zu wählen. Wenn wir einen Verein mit mindestens drei, aber maximal 100 Mitgliedern typisieren wollen, können wir dort schreiben:
type verein_t = array[3..100] of mitglied_t;
Die andere geläufige Variante von Abbildungstypen sind die assoziativen Arrays, bei denen der Programmierer den Datentyp der Indexmenge frei wählen kann. Diese assoziativen Arrays sind unter sehr vielen Namen bekannt, funktionieren aber eigentlich immer ziemlich gleich. Eine Besonderheit sind viele Skriptsprachen, bei denen die Homogenitätsanforderung, sowohl für die Indizes als auch für die Werte, aufgehoben wird. Aus Sicht des Typsystems hat die Abbildung also den Typ map(object, object): Wir stecken Objekte von irgendwelchen Typen rein, und vielleicht finden wir ein assoziiertes Objekt von irgendeinem anderen Typen.
Der geneigte Leser wird sich da Fragen: Was ist eigentlich der Unterschied zwischen einer Struktur und einer Abbildung? Die Antwort darauf ist, dass im ganz allgemeinen Fall get() und dot_operator() das gleiche sein können. Normalerweise lassen wir aber beim dot_operator nur konstante Namen zu, während wir bei get() den Index dynamisch berechnen können. Es gibt, mit Lua, sogar eine Programmiersprache, die nur einen solchen flexiblen Abbildungsttypen anbietet und sowohl Sequenzen als auch Strukturen nur Sonderfälle von Abbildungen sind.
Bisher haben wir uns nur mit Typäquivalenz beschäftigt. Die bedeutet, dass zwei Typen entweder gleich oder unterschiedlich waren. So ein bisschen gleich gab es nicht. Typsysteme, die nur, oder beinahe nur, diese Sicht auf Typen haben, nennt man monomorphe Typsysteme. Jeder Typ hat genau eine GestaltGriechisch: mono=eins, morph=Gestalt. Dies bedeutet allerdings auch, dass jede Operation und jede Funktion nur mit einem Satz an Typen aufgerufen werden kann. Sollen ähnliche Verarbeitungsschritte auf unterschiedlichen Typen ausgeführt werden, so hat man zwei Möglichkeiten: Entweder man stellt für jeden Typ einen eigenen Satz an Operationen bereit (printX_2D(), printX_3D()), was einen hohen Grad an Codeduplikation zur Folge hat. Die andere Möglichkeit ist, dass man explizit die Daten in den anderen Typ konvertiert. Bei Strukturtypen kann dies bedeuteten, dass die einzelnen Elemente ausgepackt und in ein anderes Strukturobjekt kopiert werden müssen. Das ist Fehleranfällig, langsam und führt zu einem Mehrverbrauch an Speicher.
Allerdings sind Typen vielleicht gar nicht immer so unterschiedlich, wie das eine monomorphe Sicht der Dinge nahe legen würde, sondern es gibt oft Gemeinsamkeiten. Und es sind diese Gemeinsamkeiten, die der Polymorphismus einfängt und im Typsystem formalisiert. Wenn ein Typ Polymorph ist, bedeutet das, dass derselbe Typ unterschiedliche Rollen einnehmen bzw. sich so wie ein anderer Typ verhalten kann. Am Beispiel des 3D-Punktes: Durch ignorieren der 3. Dimension kann sich jeder 3D-Punkt wie ein 2D-Punkt verhalten. Der 3D-Punkt schlüpft also in die Rolle, und betreibt Mimikry, des 2D-Punkts. Ein anderes Beispiel, dem wir nachgehen werden, ist der parametrische Polymorphismus, bei dem die Gemeinsamkeiten in einem generischen Typen gebündelt werden. Anstatt ein Listentyp jeweils für int-Liste, float-Liste, und double-Liste anzulegen, führen wir einfach den generischen Typ "Liste von beliebigen Elementen" ein.
Allerdings ist die Sache doch nicht ganz so einfach wie sie scheint, wenn wir sagen: Ein Typ soll sich halt so wie der andere Verhalten. Wenn jeder Typ einfach in die Rolle eines anderen schlüpfen könnte, würden wir alle Sicherheiten und Garantien verlieren, die uns das Typsystem versprochen hat. Daher brauchen wir Regeln, wann ein Typ wie polymorph sein kann. Und dazu brauchen wir neben der Typäquivalenz noch den Begriff der Typkompatibilität.
Wenn ein Typ S kompatibel mit einem Typ T ist, so kann S sich als T ausgeben; man kann T durch S, ohne Konvertierungen, substituieren. Je nach Kontext benötigen wir, um dies Typsicher machen zu können, unterschiedliche Formen von Kompatibilität: Wollen wir nur auf die Felder einer Struktur zugreifen, so reicht es, wenn S alle Elemente von T enthält und diese im Speicherlayout an der gleichen Stelle platziert sind. Möchte man T-Operationen auf dem S-Objekt ausführen, so müssen diese eine kompatible Schnittstelle haben. Will man das S-Objekt als vollständiges Substitut verwenden, so muss nicht nur die Schnittstelle, sondern auch das Verhalten kompatibel sein. Allerdings kann ein Typsystem nicht all diese Fälle, insbesondere den letzten, wie das Beispiel auf den Folien zeigt, abfangen.
In dieser Vorlesung wollen wir uns mit dem universellen Polymorphismus beschäftigen. Dabei geht es darum, dass die gleichen Typen in allen Kontexten gleich kompatibel sind. Beim ad-hoc Polymorphismus, der uns in den nächsten zwei Vorlesungen begegnen wird, wird in jedem Kontext einzeln festgestellt, ob die gerade vorliegenden Typen und Operationen kompatibel sind bzw. kompatibel gemacht werden können. Einen genaueren Überblick über das Thema des Polymorphismus finden Sie in dem Artikel On Understanding Types, Data Abstraction, and Polymorphism von Luca Cardelli und Peter Wegner.
Bei der ersten Form des Polymorphismus, dem Polymorphismus durch Inklusion setzen wir unsere denotationelle Brille auf und betrachten die zwei Typen S und T, deren Kompatibilität zur Frage steht. Beide dieser Typen spannen eine Menge von Objekten auf, indem sie ein Prädikat über die Zugehörigkeit zur Menge angeben (denotationelle Sicht). Alle Elemente dieser Mengen sollten sich so Verhalten wie ein T, respektive ein S. Überschneiden sich jetzt die Mengen, so gibt es Objekte, die sich sowohl wie ein T, als auch wie ein S verhalten; diese Objekte können wir also sicher substituieren. Ist die Menge S vollständig in der Menge T enthalten, so können wir nicht nur einzelne Objekte, sondern den gesamten Typen substituieren. Typ S ist ein Subtyp von Typ T.
Das erste Beispiel für so einen Polymorphismus durch Inklusion sind Subranges. Dies sind abgeleitete numerische Typen, die den Wertebereich des originalen Typen weiter einschränken. So ist jedes Element des Typen percent_t auch ein integer. Das bedeutet, dass man diese Prozentzahlen ohne Probleme dort einsetzen kann, wo eine Ganzzahl erwartet wird.
Das Umgekehrte gilt im Übrigen nicht unbedingt: Addiert man mittels der integer-Addition eine 1 auf die Prozentzahl 100, so ist das Ergebnis ganz sicher nicht mehr vom Typ percent_t abgedeckt. Daraus können wir verallgemeinert lernen, weil wir ein Gegenbeispiel gefunden haben, dass Typkompatibilität, im Gegensatz zur Typäquivalenz, nicht reflexiv ist.
Die wohl bekannteste Form des Inklusionspolymorphismus ist die Vererbung zwischen Strukturtypen, wie sie in Objekt-orientierten Sprachen vorkommt. (:public Base) gibt intentional an, dass Derived ein Subtyp von Base sein soll. Aus dieser Intention ergibt sich dann alles weitere in den Vererbungsmechanismen: Um wenigstens die grundlegendste Art der Kompatibilität, nämlich Substituierbarkeit im Speicherlayout, zu erreichen, erbt die abgeleitete Struktur alle Elemente der Basisstruktur. Weiterhin sorgt der Übersetzer dann dafür, dass die geerbten Strukturelemente an den gleichen Offsets, vom Beginn der Struktur her, zu finden sind. Um Typkompatibilität auf der Ebene der Abstraktionen zu erreichen, erbt der abgeleitete Typ alle Interfaceoperationen, die der Elterntyp aufweist. Beides, Strukturkompatibilität und Interfacekompatibilität, sind direkte Folgen unseres intentionalen Statements: Derived soll ein Subtyp von Base sein.
getX: # (Base * a0)
lw a0, 0(a0)
ret
getY: # (Derived * a0):
lw a0, 4(a0)
ret
Am gezeigten C++-Beispiel kann man die Kompatibilität im Speicherlayout relativ direkt am Assembler ablesen. Die Funktion getX(), die sowohl mit Base als auch mit Derived-Objekten aufgerufen werden kann, extrahiert das Strukturelement mit dem Namen x aus dem Objekt. Dazu dereferenziert es den übergebenen Zeiger (a0) und schlägt ein Offset von 0 auf (0(a0)), da das Feld x ganz vorne in Base- und Derived-Objekten gespeichert wird.
Alle weiteren Regeln, welche Klasse was überschreiben darf, wann welche Felder für wen sichtbar sind, das sind Sprachspezifika, die allerdings an dem grundlegenden Konzept von Vererbung nichts ändern: Wir, die Programmierer, wünschen uns, dass ein Typ ein Subtyp eines anderen wird. Es ist dann die Aufgabe der Sprache und des Übersetzers alles Notwendige zu tun, damit die daraus folgende Substituierbarkeit gewährleistet wird.
Die zweite Form des universellen Polymorphismus ist der parametrische Polymorphismus. Der Grundgedanke hierbei ist es, dem Benutzer die Möglichkeit zu geben, eigene Typkonstruktoren zu definieren und Typkonstruktoren, ganz allgemein, zu First-Class Citizens des Typsystems zu machen. Letzteres bedeutet, dass ein Typkonstruktor überall da stehen können soll, wo wir auch einen Typen hinschreiben können.
Zunächst aber führen wir generische Typen ein, die Typkonstruktoren darstellen, die der Benutzer selbst definieren kann. Dazu führen wir Typvariablen auf Sprachebene ein, welche die Argumente für unsere selbst-definierten Typkonstruktoren sind. Gewissermaßen als Funktionsrumpf des generischen Typen erlauben wir es dem Benutzer einen unvollständigen Typausdruck zu schreiben, der neben den echten Typen auch Typvariablen enthalten kann. Instanziieren wir unseren generischen Typen, so werden die übergebenen Argumenttypen an die Typvariablen gebunden, im unvollständigem Typausdruck ersetzt, und der, nun valide, Typausdruck wird zurückgegeben. Der generische Typ ist also eine Art von Schablone oder Template auf Ebene der Typausdrücke.
Im Java Beispiel lässt sich der beschriebe Mechanismus sehr gut sehen. Dort heißen generische Typen sogar Generics. Wir definieren hier einen Typkonstruktor mit dem Namen Pair, der eine Typvariable A als Argument bekommt. Diese Typvariable kommt im Rumpf des Konstruktors, der einen Strukturtyp erzeugt, zweimal vor, um zwei Strukturelemente zu typisieren. Dieser Konstruktor erzeugt also Typen, die homogen typisierte (beide Elemente haben den gleichen Typ) Paare bilden.
Wie wir im C++-Beispiel, wo generische Typen Templates heißen, sehen, können wir eine Menge an Schreibarbeit durch die Verwendung von Templates sparen. Wir müssen in unserem Programm nur jedes vorkommen von intList durch List<int> und jedes Vorkommen von charList durch List<char> ersetzen. Dies spart eine Menge an sich immer wiederholenden Typdefinitionen.
Ein weiterer Vorteil von generischen Typen sehen wir am Typen boolList: Dieser sieht beinahe so aus wie die anderen beiden Typen, allerdings ist das Feld hier anders geschrieben. Dies kann durch Unachtsamkeit oder Absicht geschehen sein, jedenfalls wird es beim Benutzer der boolList einiges an Frustration erzeugen. Bei unserem Template ist die Sache anders: Da wir immer die gleiche Schablone verwenden, um Listentypen zu erzeugen, haben diese auch immer die gleichen Felder (und Operationen) und wir können die Erwartungen des Benutzers an ein einheitliches Interface aller Listen erfüllen. Wenn wir diesem Argument genauer zuhören, dann hören wir schon den Polymorphismus durchklingen: Alle Typen, die durch den List<T> Konstruktor erzeugt wurden, haben gemeinsam, dass ihre Felder gleich heißen und in der gleichen Reihenfolge auftreten; nur die Feldtypen können unterschiedlich sein.
Darauf aufbauend können wir nun verstehen, wie parametrischer Polymorphismus funktioniert: Wir heben die Unterscheidung zwischen Typen und Typkonstruktoren auf und erlauben es, Typkonstruktoren dort zu verwenden, wo ein Typ stehen müsste. Dies erlaubt es, dass generische Typen an Argumenten oder an Variablen auftreten können. Damit können wir zum Beispiel die Funktion length(List[N]) definieren, die auf jeglicher Liste, unabhängig vom Elementtyp, die Länge bestimmen kann.
Bekommt eine Funktion einen generischen Typen als Argument, so nennen wir sie generische Funktion. Wenn wir bei diesen generischen Funktionen nach dem Funktionstyp fragen, so sehen wir, dass auch dieser selbst ein generischer Typ sein muss. So brauchen wir für den Funktionstyp von length() den Typkonstruktor type lengthType(N) = func(int, List(N)).
Daraus folgt auch, dass die selbe Typvariable in den Signaturen von generischen Funktionen mehrfach auftreten kann und so eine Kopplung zwischen Argumenttypen und Rückgabetyp entstehen kann. Dies wird gut am Beispiel von concat() deutlich: type concatType(N) = func(List(N), List(N), List(N)). Durch diese Kopplung können wir generische Funktionen hintereinander schalten um neue generische Funktionen zu erzeugen. So hätte die Funktionskomposition beider Funktionen (length(concat(x, y))) den Typen func(int, List[T], List[T]). Diese Komposition von generischen Funktionen zu komplexeren generischen Funktionen ist der Kern von funktionaler Programmierung. Wir werden diesem Thema in einem dedizierten Kapitel zu diesem Programmierparadigma noch genauer nachgehen.
Wir haben gesagt, dass alle Instanzen eines Typkonstruktors kompatibel zum Konstruktor selbst sind (List[int] ist kompatibel zu List[N]). Allerdings ist es deutlich schwieriger zu sagen, wie es um die Typkompatibilität der einzelnen Instanzen steht. Ist zum Beispiel List[int] kompatibel zu List[float]? Dies hängt maßgeblich davon ab, wie die übergebenen Typen zueinander stehen. Sind diese in keinster Weise kompatibel, so können wir auch davon ausgehen, dass die daraus instanziierten Listentypen nicht kompatibel zueinander sind. Eine List[Pferd] und eine List[Brötchen] sind sicherlich nicht durcheinander substituierbar. Beim einen kommen Pferde, beim anderen mal Brötchen raus; beide haben nichts miteinander gemein. Verwenden wir allerdings Subtypen im generischen Typ, kommt es zu drei verschiedenen Fällen: Kovarianz, Kontravarianz und Invarianz.
Bei der Kovarianz sind die instanziierten Typen in der gleichen Richtung kompatibel wie der übergebene Typ. Im Beispiel ist Cake kompatibel mit Bread (Cake -> Bread) und der dazugehörige Bäcker ist in die gleiche Richtung kompatibel: Baker[Cake] -> Baker[Bread]. Umgangssprachlich würde man sagen: Jeder Kuchenbäcker ist auch ein Brotbäcker, weil Kuchen spezielle Brote sind. Diese Art der Kompatibilität tritt ein, wenn der generische Typ nur Quelle für Objekte des Subtyps sind, da jedes einspringende Objekt sofort als Objekt der Oberklasse interpretiert werden kann. Etwas anschaulicher können wir bei jeder Methode des Bäckers, die Cake zurückliefert (Cake Baker[Cake]::bake()), einen Cast zu Bread vorlagern: ((Bread) Baker[Cake]::bake()).
Der umgekehrte Fall tritt ein, wenn der generische Typ nur eine Senke für parametrische Objekte ist. In diesem Fall können wir Kontravarianz annehmen, bei der die Kompatibilität genau entgegen der Vererbungsrichtung geht: Customer[Bread] -> Customer[Cake]. Bei der Kontravarianz ist das Argument zur Plausibilisierung genau umgekehrt: Der generische Typ ist an seinen Methodenargumenten eine Senke und dort können wir die passenden Casts einfügen: Der Subtyp Customer[Bread]::eat(Bread *) ist kompatibel mit allen Aufrufen, bei denen wir einen Cake übergeben: Customer[Bread]::eat( (Bread) cake);.
Ist der generische Typ sowohl Quelle als auch Senke für parametrische Objekte, so können wir keine Kompatibilität annehmen. In diesem Fall sind die instanziierten Typen invariant und inkompatibel zueinander.
Das Thema von Kovarianz, Kontravarianz und Invarianz ist eigentlich noch allgemeiner als nur das Zusammenspiel von Subtypen und parametrischem Polymorphismus. Es erstreckt sich auf weitere Aspekte von Typsystemen, die wir hier allerdings nicht weiter besprechen werden. Das Verbindende ist immer: Kovarianz bedeutet das Kompatibilität entlang der Vererbungsrichtung stattfindet; Kontravarianz bedeutet, dass es entgegen der Vererbungsrichtung geschieht.
Zunächst haben wir gesagt, dass jeder Typausdruck als Parameter für einen generischen Typen herhalten kann. Für viele generische Typen, vor allem für Containertypen (List[N]), macht dies auch durchaus Sinn. Allerdings gilt dies nicht für alle generischen Typen: Zum Beispiel, wenn der generische Typ die Operationen des Parametertypen verwendet (und nicht nur seine Objekte herumreicht), ist es nötig, dass der übergebene Typ auch diese Operationen bereitstellt. Im Beispiel könnte man sagen: Der Baker[T] wird seine Gebäcke T fragen, bei welcher Temperatur sie gebacken werden wollen (T::degrees()). Da ein Car allerdings diese Schnittstelle nicht anbietet, ist der Typ Baker[Car] quatsch.
Um dieses Problem anzugehen, bieten viele polymorphe Typsysteme noch die Möglichkeiten Einschränkungen für Typparameter anzugeben. So ist es bei Java möglich zu fordern, dass ein Parameter Unter- (oder Überklasse) einer bestimmten Klasse sein muss (T extends Bread). Es wird also entlang der Vererbungshierarchie eine Einschränkung der möglichen Belegungen von T vorgenommen.
Wenn wir jetzt einen Schritt zurücktreten und uns die denotationale Interpretation von Typen (Typen sind ihre Objektmenge) in Erinnerung rufen, so sehen wir, dass wir nur Typen über Typen geschaffen haben. T extends Bread ist ein Typ, der eine Menge von Typen als Objektmenge hat.
Syntaktisch noch deutlicher kann man dies bei Rust und Type Traits sehen: Dort wird der Typtyp explizit angelegt und trait genannt. Im Fall von Rust ist dieser Trait noch mit einem gebotenem Interface verbunden. Mittels impl können Typen explizit zu einem Traits hinzugefügt werden (wobei das Interface entsprechend implementiert werden muss). Wenn wir uns jetzt die Signatur von fn bake anschauen, dann sehen wir die parallele Konstruktion in der Parameterliste des Typen und der Funktion: Bakable ist der Typ des Typparameters T, und T ist der Typ des (echten) Parameters b. Wir müssen uns nur die spitzen Klammern <> als runde Vorstellen ().
Bisher haben wir uns hauptsächlich mit Typen und der Beziehung zwischen unterschiedlichen Typen auseinandergesetzt, und die Verwendung von Typen in einer Programmiersprache haben wir außen vor gelassen. Nur am Rande fiel der Begriff Typsystem, der beschreibt, wie Typen in einer Sprache verwendet werden, welche Garantien wir durch ihre Verwendung erlangen und was wir notieren müssen, um in den Genuss der Vorteile zu kommen. Im Folgenden wollen wir uns kurz damit beschäftigen, was ein Typsystem ausmacht und wie wir das Typsystem einer Sprache charakterisieren können.
Das Offensichtliche an einem Typsystem ist, welche eingebauten Typen es gibt, welche Typkonstruktoren bereitstehen, und ob wir die eine oder andere Form der Polymorphie vorliegen haben. Alle Aspekte sind Teil der Spezifikation der Sprache und müssen eindeutig festgelegt sein. Weiterhin kommen jedoch weitere Eigenschaften eines Typsystems vor, die gerne zur Charakterisierung der ganzen Sprache herhalten müssen. Ein Beispiel für eine solche Charakterisierung wäre: "Python ist eine dynamisch, aber strikt, typisierte Sprache". Wir wollen uns hier auf zentrale Aspekte fokussieren: Typsicherheit und Typannotationen.
Unter Typsicherheit versteht man, dass ein Programmierer die Garantien eines Typsystems nicht, oder nur explizit, umgehen kann. Eine Sprache, die eine hohe Typsicherheit anpreist, verspricht, dass es niemals passieren kann, dass wir ein Car Objekt als ein Bread Objekt ausgeben können; beispielsweise durch reinterpretation des Speichers. Umso strikter, oder stärker, eine Sprache typisiert ist, umso strikter hält sich das Programm (oder der Interpreter) auch zur Laufzeit an die Regeln des Typsystems und lässt es, zum Beispiel, nicht zu, dass ein Objekt in einer Variable mit inkompatiblem Typ gespeichert wird.
Viele Sprachen, insbesondere die systemnahen Programmiersprachen, wie C/C++ oder Rust, brauchen allerdings das kontrollierte Umgehen des Typsystems, da sie direkt mit Speicher und mit Hardware interagieren müssen. Diese Reinterpretation eines Objekts geschieht dort darüber, dass wir einen Pointer auf ein Objekt von Typ A zu einem Pointer auf den Typen B durch einen Cast umwandeln. Da normalerweise alle Pointer gleich groß sind (Maschinenwortbreite), geht dies normalerweise ohne weitere Schwierigkeiten. Allerdings sind solche reinterpret_cast<B>(a) Operationen gefährlich und können daher in modernsten Sprachen wie C# oder Rust nur in explizit annotierten unsafe {} Blöcken verwendet werden.
Beim Thema der Typannotationen gibt es zwei Varianten: Während die statische Typisierung vom Programmierer verlangt, Typen statisch an Variablen zu annotieren, kann man bei der dynamische Typisierung vollständig darauf verzichten. Bei der statischen Typisierung gibt es weiterhin die Variante, dass man Annotationen manchmal weglassen kann, wenn der Sprachprozessor den Typen einer Variable aus dem Kontext heraus durch Typinferenz herausfinden kann.
Der Unterschied zwischen statischer und dynamischer Typisierung ist, welche Typen mit einer Variable verbunden sind. Hierbei ist wichtig, dass es einen Unterschied zwischen einer Variable und ihrem Inhalt gibt: Variablen sind statische Programmelemente (mit einem Namen), in denen wir, zur Laufzeit/dynamisch ein Objekt speichern können. Die abgelegten Objekte haben immer, auch bei dynamischer Typisierung, einen TypenDie Striktheit des Typsystems entscheidet dann darüber, wie sehr wir uns an diesen Typen halten.. Dieser Typ des gespeicherten Objekts wird zum dynamischen Typen der Variable. In dynamisch-typisierten Sprachen hat jede Variable nur diesen dynamischen Typen.
In statischen-typisierten Sprachen haben Variablen zusätzlich einen statischen Typen, den wir in den Programmtext schreiben. Wir deklarieren die Variable mit einem gewissen Typen, der sich niemals ändert und fest an der Variable hängt. Eine statische-typisierte Sprache garantiert, dass der dynamische Typ einer Variable immer kompatibel zu ihrem statischen Typ ist, sofern man das Typsystem nicht absichtlich umgangen hat.
Am Beispiel der statischen Typisierung kann man gut den Unterschied zwischen den, häufig gebrauchten, Worten "statisch" und "dynamisch" aufzeigen. Diese Unterscheidung ist zentral für Programmiersprachen und Übersetzer: Der dynamische Typ einer Variable kann immer erst zur Laufzeit festgestellt werden; er hängt am Maschinenzustand der virtuellen Maschine und es kostet oft Laufzeit ihn zu ermitteln, weil man im Speicher nachsehen muss. Der statische Typ der Variable steht schon zur Übersetzungszeit fest. Der Übersetzer ermittelt ihn in der semantischen Analyse und wir können bereits zur Übersetzungszeit Entscheidungen treffen, die uns später, zur Laufzeit, Rechenzeit sparen. Weiterhin können wir mit statischen Typen Garantien über jede möglich Ausführung eines Programms geben, wo der dynamische Typ nur situativ, für eine Ausführung, gültig ist.
Da statische Typisierung oft eine Menge Schreibarbeit bedeutet, haben Übersetzer gelernt, statische Typen automatisch aus dem Programmkontext zu ermitteln (= zu inferieren). Bei der Typinferenz betrachtet der Übersetzer alle Verwendungen einer Variable und überlegt sich, welcher statische Typ denn passen könnte. Am offensichtlichsten ist dies bei der Initialisierung einer Variable:
object_t create_object(); auto a = 23; auto b = create_object();
Bei der Variable a kann der Übersetzer aus dem statischen Typen des Literals 23 (Literale haben immer einen bekannten statischen Typen) ermitteln; bei b kann er dies aus dem Rückgabewert der Funktion create_object(). Mit der Technik der Unifikation, die wir uns später anschauen wollen, werden wir die Übersetzertechnik kennenlernen, die hinter der Typinferenz steht. Für die Verwendung von Typinferenz auf Sprachebene müssen wir allerdings nur wissen: Typinferenz bedeutet, dass der Übersetzer den statischen Typen einer Variable ausrechnet.
Records, oder Verbunddatentypen, treten in vielen Sprachen auf. In C heißen sie structs.
Siehe Lexer Hack.
Integer Overflows sind allerdings ein schwerwiegendes Problem in real existierender Software. Understanding Integer Overflow in C/C++, Dietz et. al., TOSEM 2015
Griechisch: mono=eins, morph=Gestalt
Die Striktheit des Typsystems entscheidet dann darüber, wie sehr wir uns an diesen Typen halten.
