Algorithmen und Datenstrukturen 2
Die Vorlesung Algorithmen und Datenstrukturen 2 ist eine Wahlpflichtveranstaltung für Studierende der Informatik, Wirtschaftsinformatik, Informations- und Systemtechnik; außerdem ist sie offen für interessierte Studierende anderer Studiengänge.
Algorithmen sind das methodische Herz der theoretischen und praktischen Informatik; Datenstrukturen ermöglichen die effiziente Umsetzung von Algorithmen und den effizienten Zugriff auf Input- und Outputdaten. In dieser weiterführenden Vorlesung werden die folgenden grundlegenden Begriffe erarbeitet:
- Elementare Aspekte zu Heuristiken
- Exakte Verfahren: Dynamic Programming, Branch-and-Bound
- Approximationsalgorithmen
- Komplexitätsaspekte
- Hashing
Literatur
- Skript: Zu dieser Vorlesung gibt es ein MANU-SKRIPT. (Stand: 21.06.21)
- Achtung: Das ist vorläufig und in diesem Semester noch in laufender Entwicklung!
- Literaturempfehlung (englisch): Silvano Martello, Paolo Toth: Knapsack Problems (PDF!), Wiley and Sons, 1990
- Literaturempfehlung (englisch): Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein: Introduction to Algorithms, MIT Press, 2001
- Literaturempfehlung (deutsch): Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein: Algorithmen – Eine Einführung, Oldenbourg Wissenschaftsverlag, 2010
Hausaufgaben
Für alle Hausaufgaben gelten die Punkte auf dem Hinweiszettel. Eine Liste mit den e-Mail-Adressen der Tutor*innen gibt es hier.
- Blatt 1: HIER. Abgabe bis 11.05.21 23:59 Uhr
- Blatt 2: HIER. Abgabe bis 01.06.21 23:59 Uhr
- Blatt 3: HIER. Abgabe bis 15.06.21 23:59 Uhr (Entscheidungsbaum: PDF, IPE, SVG) (Aktualisierte Version vom 10.06.21: Hinweis zu Aufgabe 2 korrigiert.).
- Blatt 4: HIER. Abgabe bis 29.06.21 23:59 Uhr
- Blatt 5: HIER. Abgabe bis 13.07.21 23:59 Uhr
Präsenzblätter
Merkzettel: Pseudocode, Beweistechniken, Wachstum von Funktionen.
Diese Blätter werden nicht abgegeben und werden in den kleinen Übungen besprochen. Um gemeinsam an Dokumenten zu arbeiten bieten sich folgende Dienste an: Google Docs (Du kennst Alternativen? Lass es uns wissen, dann können wir die Liste erweitern!)
- Blatt P0: HIER. (Besprechung 05.05.21-07.05.21)
- Blatt P1: HIER. (Besprechung 19.05.21-21.05.21)
- Blatt P2: HIER. (Besprechung 09.06.21-11.06.21)
- Blatt P3: HIER. (Besprechung 23.06.21-25.06.21)
- Blatt P4: HIER. (Besprechung 07.07.21-09.07.21)
- Blatt P5: HIER. (Besprechung 21.07.21-23.07.21)
Vorlesungen
-
Online-Prüfung Informationen (Wiederholungsprüfung)Liebe Studierende, hier eine Reihe von Informationen zur Vorbereitung der AuD2-Prüfung am 25.02.22. Bitte lesen Sie diese sehr sorgfältig! Sollten …
Online-Prüfung Informationen (Wiederholungsprüfung) Weiterlesen »
-
Online-PrüfungWichtige Informationen zur Online-Prüfung.
-
Vorlesung 13In dieser letzten Vorlesung des Semesters rekapitulieren wir noch einmal das Semester und geben ein paar Ausblicke in weiterführende Themen.
-
Vorlesung 12
In dieser Vorlesung beschäftigen wir uns etwas näher mit Hashfunktionen und Lösungsstrategien für auftretende Probleme wie Kollisionen. Außerdem schauen wir uns weitere Anwendungen für Hashfunktionen an. -
Übung 6
In dieser Übung beschäftigen wir uns noch einmal mit Hashing, bevor wir einen kurzen Rückblick auf das vergangene Semester machen. -
Vorlesung 11
In dieser Vorlesung wenden wir uns dem Thema Hashing zu. -
Vorlesung 10
In dieser Vorlesung machen wir einen Exkurs und beschäftigen und mit Optimierungsmethoden für mehrdimensionales Packen. -
Übung 5
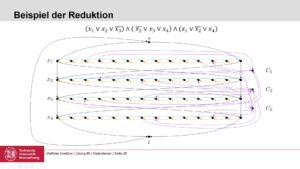In dieser Übung beschäftigen wir uns mit dem Approximationsalgorithmus Greedyk für das Knapsack-Problem. Außerdem schauen wir uns mit Vertex-Cover noch ein neues Problem an. -
Vorlesung 9
In dieser Vorlesung analysieren wir die Komplexität einiger uns bekannter Probleme und besprechen die daraus resultierenden Konsequenzen. -
Vorlesung 8
In dieser Vorlesung beginnen wir uns mit weiterführenden Aspekten zur Komplexität zu beschäftigen. Dabei lernen wir die verschiedenen Komplexitätsklassen kennen und diskutieren deren Eigenschaften und Beziehungen.