A swarm of many simple robots that have only local perception can in some scenarios be superior to a much more powerful but single robot. Inspired by nature, robot swarms can be robust, flexible, and scalable. More precise, they can tolerate the loss of individuals, quickly adapt to changes, and work on arbitrary sizes.
Consider a swarm of robots that needs to remain connected. There is no central control and no knowledge of the overall environment. This environment is hostile: The swarm is being pulled apart by external forces, stretching it into a number of different directions, so it is in danger of breaking up. Individual robots are weak, with limited sensing, limited communication, and limited connectivity; even worse, each robot’s expected lifetime is limited by random, permanent failures, which may destroy connectedness and functioning of the swarm as a whole. How can we achieve coordinated dynamic swarm behavior without centralized coordination? How can we employ each robot as much as possible, without depending on it if it fails? How can we balance overall flexibility and robustness to deal with the hostile environment?
We propose a set of local continuous algorithms that together produce a generalization of a Euclidean Steiner tree. At any stage, the resulting overall shape achieves a good compromise between
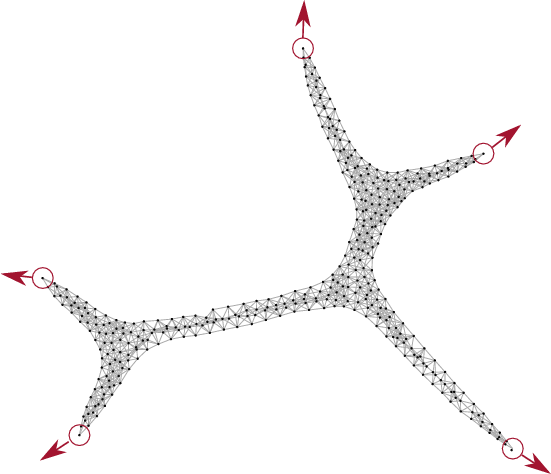
We are building upon the flocking algorithm of Olfati-Saber, the boundary detection of McLurkin and Demaine, and especially the boundary tension of Lee and McLurkin (which itself builds upon the previous two). The boundary tension is also the origin of the Steiner tree shape of the swarm.
We added two main components
Consider a large company of n robots after deployment. They are scattered across a geometric region. While the swarm is still connected in terms of communication, it lacks central control; and while each of the robots carries a unique ID, none of them has information about the actual range of labels. How can we get the group into an organized arrange- ment: an equally spaced array between the positions of the robots with minimum and maximum label? Not only does this demand dealing with the possibly complicated geometric arrangement in a distributed fashion; it also involves sorting them by label, which already requires n log n in a centralized setting. Furthermore, what are the achievable time until completion, required communication, and distance traveled?
We describe a distributed method to accomplish these goals, without using central control, while also keeping time, travel distance and communication cost at a minimum. We proceed in a number of stages (leader election, initial path construction, subtree contraction, geometric straightening, and distributed sorting), none of which requires a central authority, but still accomplishes best possible parallelization. The overall arraying is performed in O(n) time, O(n^2) individual messages, and O(nD) travel distance. Implementation of the sorting and navigation use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.
Technische Universität Braunschweig
Universitätsplatz 2
38106 Braunschweig
Postfach: 38092 Braunschweig
Telefon: +49 (0) 531 391-0